Ciao Igino,
ormai di corsi e seminari su questi temi ne ho tenuti talmente tanti che mi diventa perfino difficile trovarne uno specifico, come quello citato da Mirko. In ogni caso, sì, come dice lui, il corso 35 - Topografia-Catasto-Riconfinazioni - Mod. 3 - Rilievi GPS e integrati con TS è una buona base di partenza se vuoi farti le ossa sul GPS. Dopodiché, se hai passione e vuoi andare a fondo, il corso per farlo è 128 - Geodesia e Cartografia per Geometri, tenuto dai Prof. Maseroli e Surace. È proprio su quest’ultimo corso (suddiviso in tre moduli) che io ed altri colleghi abbiamo postato diversi esempi su Excel e CAD dei vari calcoli ed elaborazioni apprese dai docenti. Se mai affronterai questi argomenti, trovi tutti i link in quest’altro topic:
Esercizi ed esempi del corso Geodesia e Cartografia per Geometri
Per avere una prima infarinatura ti consiglio di guardare i video gratuiti di www.topgeometri.it che sono appunto i seminari gratuiti di cui accennava Mirko. Li trovi al menù RISORSE GRATUITE | Video gratuiti, scendi nella pagina fino al titolo Topografia dove vedi alcuni dei video della raccolta. Se poi clicchi su Guarda tutti i video su YouTube entri sull’intera playlist di YouTube nella quale puoi trovare quelli che trattano il GPS.
Ma ovviamente quanto sopra richiede molto tempo e dedizione, per cui non voglio certo darti solo quelle indicazioni che valgono semmai per una tua futura crescita professionale. Cercherò quindi di rispondere in breve al tuo quesito circa lo spostamento in locale della base GPS.
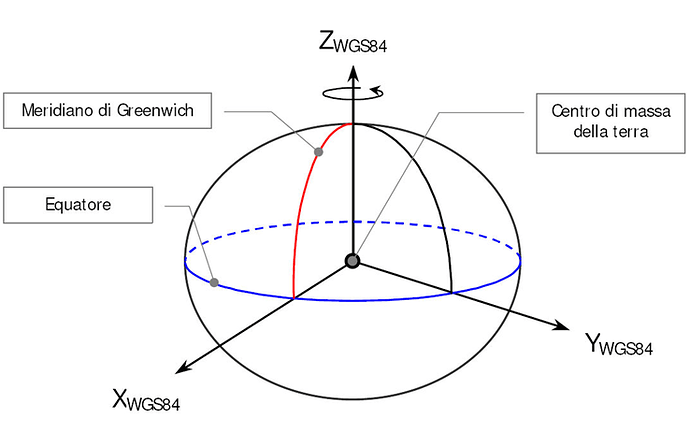
Allora, il GPS si basa su un sistema di assi cartesiani X-Y-Z con origine sul centro (di massa) della terra con l’asse Z sul polo Nord, l’asse X sull’intersezione tra l’equatore e il meridiano di Greenwich e l’asse Y a completare la terna destrorsa (in direzione Est):
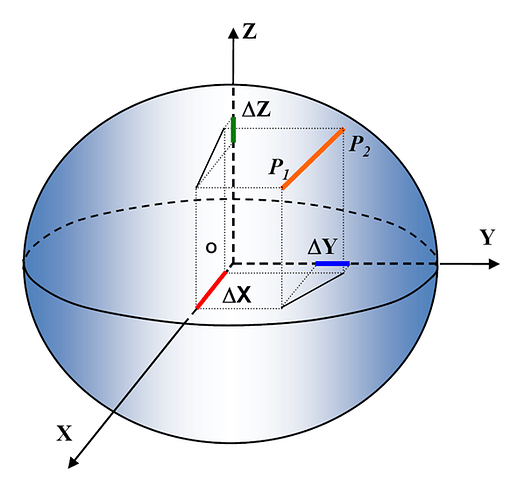
La strumentazione GPS misura la baseline cioè la congiungente nello spazio (vettore 3D) tra la base GPS (P1 nell’immagine che segue) e il punto rilevato (P2). La baseline è definita dai tre delta X-Y-Z tra i due punti, cioè dalla differenza nei tre assi tra la posizione del punto e quello della base:
Questo significa che le coordinate dei punti GPS sono direttamente sommabili tra loro. Ad esempio, sempre con riferimento alla figura qui sopra, se noi vogliamo far diventare P2 la base e P1 il punto, basterà invertire il segno dei delta X-Y-Z.
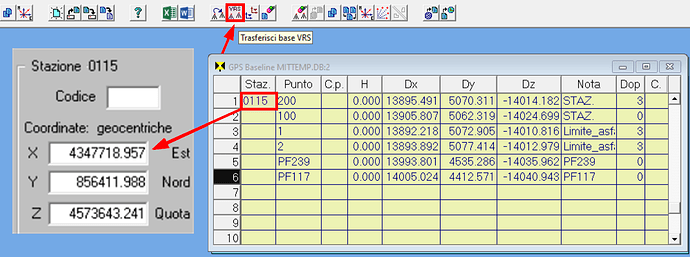
Quindi, per portare la base GPS in locale, nei rilievi NRTK appoggiati alle reti di stazioni permanenti, è sufficiente ricalcolare i delta X-Y-Z rispetto al punto assunto come nuova base anziché rispetto alla base originaria. Ad esempio, guarda questo rilievo:
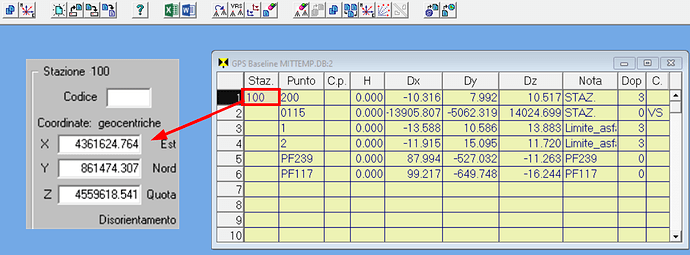
I delta X-Y-Z dei punti rispetto alla base 0115 sono molto elevati (13 km, 5 km, 14 km), questo perché la base è una stazione delle rete NRTK molto distante dal luogo del rilievo. Questa base 0115 ha le coordinate geocentriche (rispetto al sistema cartesiano di cui sopra) che vedi evidenziate. Ora attivo la funzione Trasferisci base VRS (è il mio software Geocat) e gli impongo di invertire tale base con il punto 100 del mio rilievo, cioè porto la base in locale. Ottengo questo risultato:
Come vedi, adesso la base è diventata il punto 100, mentre la ex base 0115 è diventato un punto rilevato. Adesso l’unico punto ad avere delta di km è la ex base 0115 (che in genere viene addirittura eliminata dal rilievo) mentre tutti gli altri punti hanno delta molto contenuti perché riferiti al punto 100 del rilievo locale.
Che calcolo è stato fatto?
Semplice: dapprima si sono calcolate le coordinate geocentriche di tutti i punti a partire da quelle della base 0115 sommando i delta riferiti ad essa, trovando così le geocentriche del punto 100. Poi si sono calcolati i delta riferiti a tale punto per differenza tra le geocentriche degli altri punti e quelle del punto 100. Esempio per la sola X del punto 200:
X geoc. 0115 = 4347718.957
+ delta X 100 = 13895.491
X geoc. 100 = 4361614.448
X geoc. 0115 = 4347718.957
+ delta X 200 = 13905.807
X geoc. 200 = 4361624.764
delta X 200-100
4361624.764 -
4361614.448 =
----------------------
10.316
Spero che quanto sopra sia sufficientemente chiaro, altrimenti chiedimi pure.