Ciao Paolo.
sì, le tue convinzioni sono tutte valide, io le condivido in toto e cerco di farle condividere anche dai colleghi del forum; purtroppo non sempre riuscendoci come potrai vedere dall’altra discussione ( Quale georeferenziazione usare per le mappe d’impianto nelle riconfinazioni? ) in cui alcuni hanno detto di prediligere altre georeferenziazioni più “moderne”, senza capire che alcune di quelle tecniche di fatto scindono quel legame, invece indissolubile, che tu hai ben messo in evidenza, cioè quello tra il reticolo parametrico e i punti presenti al suo interno.
Non solo, ma alcune di quelle georeferenziazioni, come quelle denominate “Griglia” o quelle di ricampionatura dei pixel, o ancora quelle polinomiali, “scavalcano” il singolo quadrante parametrico e operano sull’intera maglia dei parametri con il rischio, che tu hai altrettanto ben descritto, cioè che un punto in prossimità di un parametro passi dal quadrante originario a quello limitrofo.
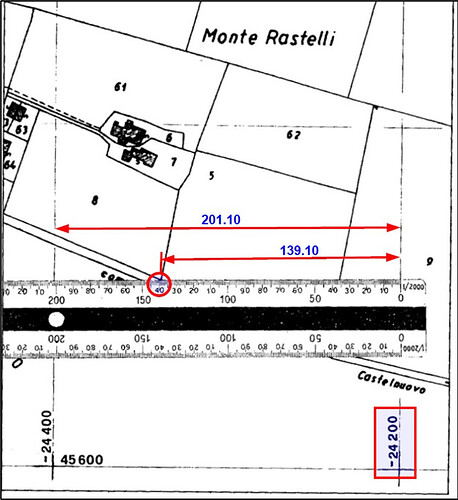
È proprio seguendo le tue stesse convinzioni che io (ma fortunatamente anche molti altri colleghi) ho sempre sostenuto che non si deve assolutamente derogare dal Metodo Tani, espressione divenuta popolare a seguito della procedura che Pier Domenico Tani ha descritto nel suo libro Aspetti tecnici dell’azione di regolamento di confini – II edizione, a pag. 62, dove riportava il seguente esempio di prelievo delle coordinate di un punto dalla mappa cartacea:
-
Con lo scalimetro si misura dapprima la distanza tra i due parametri all’interno dei quali ricade il punto di cui prelevare le coordinate, valore pari a:
201.10 -
Si misura poi la distanza del punto P dal parametro di riferimento, nell’esempio pari a:
139.10 -
Si calcola il coefficiente di compensazione facendo il rapporto fra la distanza nominale tra i parametri e quella misurata, dove per “distanza nominale tra i parametri” si intende ovviamente quella che la mappa dovrebbe presentare se non avesse subìto alcuna deformazione.
coefficiente di compensazione = 200 / 201.10=0.9945 -
Si determina la distanza compensata di P dal parametro:
distanza compensata = 139.10 • 0.9945 = 138.34 -
Si calcola la Est di P sommando algebricamente la distanza compensata a quella del parametro di riferimento:
Est= -24200 + (-138.34) = 24338.34
Io ho sempre seguito questo criterio e, con la mia georeferenziazione Parametrica, ho soltanto affinato il calcolo grazie al fatto che la disponibilità delle mappe su file raster permette un calcolo matematico più spinto. Ma il criterio rimane quello del Tani, cioè si basa su questi presupposti:
-
Il quadrante parametrico (originariamente di 200 x 200 m) è la zona più ristretta della quale disponiamo delle coordinate numeriche, pertanto dobbiamo agire sempre e solo su tale area.
-
Ciascun punto di mappa va trattato all’interno del quadrante parametrico in cui ricade. Non vanno quindi mai utilizzati algoritmi che “mettono insieme” i quadranti.
-
All’interno di un singolo quadrante la curvatura che hanno subito i parametri è di fatto irrilevante (può invece non esserlo se consideriamo i parametri sull’intero foglio). Pertanto, all’interno di un singolo quadrante i parametri possono essere ragionevolmente considerati rettilinei anche se, per effetto della deformazione, non sono rimasti paralleli tra loro.
Sulla base di quanto sopra, e con riferimento all’animazione che segue, la Parametrica esegue questo calcolo:
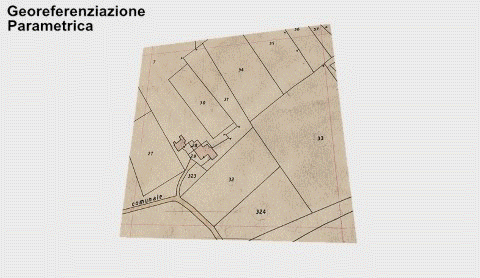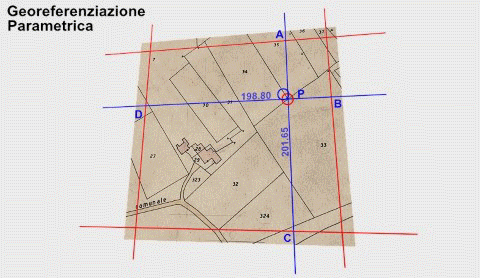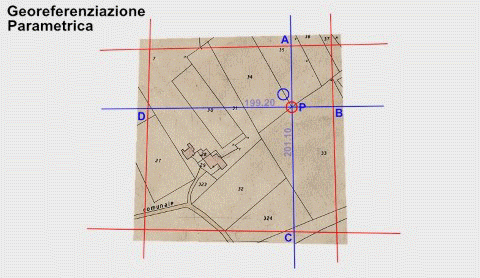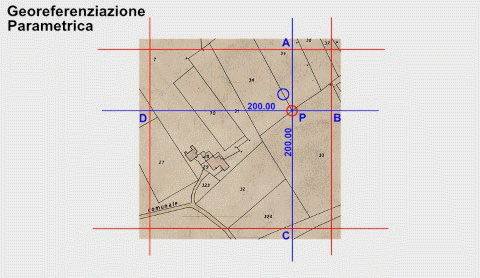
-
Si determinano le rette (equazioni) dei parametri a partire dalle coordinate dei crocicchi.
-
Dalle rette dei parametri si ricavano le coordinate delle intersezioni tra i due parametri orizzontali e tra i due parametri verticali.
-
Si calcolano le coordinate dei punti A, B, C, D per intersezione delle rette dei parametri con le rette A-C e D-B.
-
Le due distanze A-C e D-B, normalmente diverse da 200 m per effetto della deformazione, vengono riportate a 200 m, trovando così la piu verosimile posizione originaria del punto P e quindi le sue coordinate mappa.
I colleghi che si lasciano sedurre dalle georeferenziazioni “moderne”, come la ricampionatura dei pixel (tecnica adottata anche dall’AdE), pensano invece che il poter oggi disporre delle mappe d’impianto su file digitale possa consentirci di applicare tutte le possibili tecniche, appunto, di ricampionatura dei pixel (ce ne sono a decine). Il loro (grave) errore concettuale è quello di trattare i file raster come se le mappe fossero nate già come immagini fin dall’inizio (come ad esempio per il raddrizzamento di foto di facciate prospettiche), senza invece considerare che le mappe d’impianto sono nate su carta e tali sono rimaste per decenni.
In pratica, questi colleghi pensano che l’attuale disponibilità delle mappe raster possa esonerarci dal tenere in assoluta considerazione la genesi stessa delle mappe cartacee (vedi qui sotto) potendo viceversa sbizzarrirci ad applicare l’algoritmo che più ci piace o quello implementato dal software che si utilizza, qualsiasi esso sia.
A tal proposito riporto qui il link al brano del mio libro Tecniche di riconfinazione in cui ho descritto la genesi delle mappe d’impianto: